Enhancing MPPT performance for partially shaded photovoltaic arrays through backstepping control with Genetic … – Nature.com

Demand for energy on a worldwide scale is fast altering as a result of recent rapid distribution, industrial growth, and urban planning, while natural energy resources such as gas and oil are running out and prices are rising. Now we have to add environmental concerns to our energy concerns^1,2. We now know that a change in Earth’s surface climate has resulted from the excessive accumulation of greenhouse gases (GHG) in the atmosphere³. The result is a global increase in surface temperature. Researchers are inspired to enhance resource management and adopt renewable energies by a number of causes, including the increasing cost of energy and stricter regulations enacted to protect the environment^4,5.

All forms of renewable energy trace back to the sun, making it the most potent source for powering Earth. Solar air currents produce wind, light, and heat, while hydrologic cycles drive dam turbines. Solar energy fuels all food chains, ensuring the sustenance of life. The prospect of harnessing this energy captivates human curiosity^6,7. Solar energy stands as the most abundant on Earth. Despite humans consuming 10 billion metric tons of oil annually^8,9, this represents less than 3% of the daily solar energy available. These energy sources are sustainable for at least 4.5 billion years, as the sun consistently provides its energy. An additional benefit is their contribution to mitigating global warming.

Solar energy is cheaper because panel production and maintenance have dropped dramatically in the past decade. The photovoltaic industry dominates renewables. Worldwide solar panel installations exceeded 115 GW in 2019. It’s 12% higher than 2018. Solar PV installed 627 GW worldwide in 2019^10,11. PV generators or modules generate electricity by connecting photovoltaic cells in series or parallel. Each series cell receives the same current, and its voltages determine its characteristic. Parallel cells have a constant group voltage and a collective property of the sum of their currents. Irradiance and temperature greatly impact PV cell and generator performance. Weather determines power point location. MPPT maximizes solar array output^12,13.

According to literature, researchers used online, offline, and hybrid MPPT. Offline methods that use photovoltaic panel properties and solar irradiation measurements like V_OC and I_SC^14,15 don’t measure extracted power, which is inaccurate when atmospheric conditions change rapidly. Researchers use simple, easy-to-implement online methods like P&O^16,17 and INC^18,19. Small photovoltaic voltage disturbances by the P&O algorithm change PV module power. Measure solar cell power output after each disturbance. If power increases, the controller searches and jumps again. If power is low, the controller switches search directions and performs. This method always maximizes power, but even with constant light, output power fluctuates. Since the power-voltage derivative is zero at MPP, the INC method, an enhanced P&O method, can calculate MPP without oscillation. Maximum power point tracking under rapidly changing irradiation conditions is better than P&O. To maintain MPP functionality during irradiation, both strategies iteratively run the MPP tracker’s microprocessor. P&O and INC are susceptible to rapid convergence and large irradiance changes²⁰.

PV modules experiencing partial shading receive uneven sunlight, leading to the emergence of multiple P–V peaks. These peaks signify both local and global maximum powers, a departure from the uniform sunlight conditions^21,22. The P&O and INC approaches exhibit fluctuations due to the limited nonlinear capacity, and the localization of GMPP becomes unattainable. Staying at the Local Maximum Power Point (LMPP) is a consequence, potentially reducing power output.

Given the constraints of P&O and INC MPPT, researchers have devised hybrid approaches to achieve accurate MPP tracking. Controller-based algorithms such as P&O, PI, PID, and INC^23,24,25,26 have been employed. While PV generator nonlinearity and power electronic converter time variance are well-understood, it’s essential to note that PI and PID are linear controllers^27,28. Consequently, nonlinear methods prove more effective in ensuring PV system dependability amid changing operating conditions and optimizing tracking performance. Scientists have turned to nonlinear SMC/BSC controllers to address this need.

In the realm of closed-loop controllers, having a dependable reference is crucial. In this regard, the maximum power voltage serves as our benchmark, and diverse methods can be employed to generate it. P&O BSC²⁹ and INC BSC³⁰ have incorporated nonlinear controllers, showcasing improved tracking and rapid convergence. Despite these advancements, these approaches still face challenges in tracking the GMPP, limiting their reference applicability.

Numerous power control researchers have leveraged optimization algorithms and controllers to enhance their findings. In Reference³¹, a backstepping controller with ANNPSO is proposed to track the maximum power point under partial shading, achieving global maximum power point tracking without oscillations. Compared to other controllers, this method tracks the reference voltage in 20 ms and gains 5 W. Reference³² presents a MATLAB/Simulink mathematical model for energy losses and photovoltaic module power analysis, revealing that uneven illumination can lead to power drainage from more intensely illuminated cells. Bypass diodes, while disabling ‘hot spots,’ result in panel energy wastage. Reference³³ suggests a hybrid approach to address partially shaded PV array power mismatch losses, utilizing a magic square array configuration and differential evolution-based adaptive perturb and observe maximum power point tracking. The PV panels are repositioned in a magic square to find the global peak power point, reducing partial shading power losses. Experimental and simulation results indicate a 19% and 20% boost in power output for uniform and nonuniform shading^34,35.

Knight’s Tour Magic square (KTM) and Doubly Even-order Magic square (DEM) shadow dispersal techniques in PV arrays are explored in Reference³⁶, comparing them to total-cross-tied, odd-even, and odd-even-prime configurations. The proposed techniques enhance global maximum power (GMP) by 42.67% for asymmetric arrays and 26.43% for symmetric arrays. In Reference³⁷, an interleaved soft-switched boost converter (ISSBC) and photovoltaic panel are introduced for distributed maximum power point tracking (MPPT) in partial shadow conditions. ISSBC is managed by a PSO–ANFIS-trained adaptive neuro fuzzy inference system. A single-phase cascaded H bridge five-level inverter (CHI) with selective harmonic elimination eliminates seventh-order harmonics after the ISSBC. The proposed method reduces ripple and handles higher currents with low switching losses. Simulations and experiments demonstrate that PSO–ANFIS outperforms other MPPT control schemes.

Given the plethora of MPPT (Maximum Power Point Tracking) methods, researchers and practitioners in PV (photovoltaic) systems have undertaken surveys or comparisons³⁸. The extracted power in energy production often falls below the MPP (Maximum Power Point), leading to significant power losses. This method proves ineffective when tracking the MPP in the presence of partial shading or damage to PV cells. While fuzzy logic and artificial neural networks can track MPPs, their effectiveness relies on well-designed inference mechanisms, rule bases, and offline statistics training data processes. The controller, incorporating operator skills, inference rules, and membership functions, may encounter faults^39,40.

In the optimization of MPPT in partial shade, modern heuristics are employed. Simulations have validated the applicability of the Ant Colony-based optimization technique in⁴¹, but it’s hardware implementation poses challenges. The fuzzy logic system, combined with an additional scanning scheme in⁴², converges to the final optimal point. A novel global MPPT technique⁴³ necessitates intricate mathematical procedures, making implementation difficult. “Submodule-Integrated Distributed Maximum Power Point Tracking for PV Applications” is discussed in⁴⁴.

Hybrid solutions, combining techniques to address their respective weaknesses, emerge as practical approaches to tackle complex real-world problems^45,46. Shadow-related issues gain significance due to the nonlinear nature of shadow-induced production losses⁴⁷.

The same principles are relevant to the hybrid GA-BSC methodology presented in this paper. To emulate PV shadowing and mirror real-world scenarios accurately, a nonlinear controller is employed. Our goal is to achieve GMPP-compliant regulation in the PV system. In order to adjust the (DC-DC) converter duty cycle and monitor the reference voltage, the GA is tasked with initially generating the GMPP reference voltage and subsequently determining the optimal BSC parameters, (K_{1}) and (K_{2}). Our model yields benefits by simulating 33% less power loss, showcasing a capitalization that is less than three times compared to alternative stability methods. Notably, our model exhibits optimal robustness.

This paper will be organized as described below. In the second part, we go into the SEPIC and PV module models. In the third section, we outline the strategy we recommend. The results of the simulation and a summary are presented in Parts four and five, respectively.

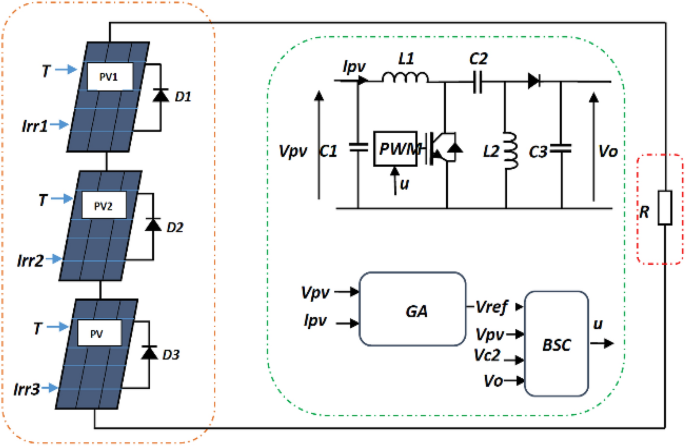
The photovoltaic system described in this study is illustrated in Fig. 1. It comprises three 55 W modules connected in series to form a solar panel. Additionally, the system includes a DC–DC converter of the SEPIC type and a resistive load with a value of 150 Ω.

Modelling of a photovoltaic module

The single diode model is commonly employed for simulating solar modules due to its inherent simplicity⁴⁸. However, due to the relatively high absolute errors of current and voltage, there is a possibility of degradation in the accuracy of the model^49,50. Therefore, the inclusion of the double diode model is considered in this study to ensure accurate modeling.

The subsequent equation can be utilized to articulate the output current of a photovoltaic cell:

In the given context, the symbols “I” and “V” represent the current and voltage of the PV module, respectively. “(I_{ph})” represents the photocurrent, while “(R_{s})” and “(R_{p})” denote the series resistance and shunt resistance of the PV module. Additionally, “(I_{D1})” and “(I_{D2})” represent the current flowing through diodes 1 and 2, respectively:

Subsequently, through the substitution of Eq. (2) and Eq. (3) into Eq. (1), the resulting expression is obtained:

The coordinates ((I_{01}), (I_{02})) represent the diode saturation currents, while ((a_{1}), (a_{2})) represent the ideality factors. The equation “(V_{{text{t}}}) = kT/q” defines the thermal voltage, where T represents the temperature of the cell in Kelvin (K), q represents the charge of an electron (1.6 × 10^ (−19)), and k represents the Boltzmann constant^51,52.

In the domain of photovoltaic modeling, the parameters (a_{1}), (a_{2}), ({ }I_{01}), ({ }I_{02}), (I_{{{text{ph}}}}),({ }R_{{text{s}}}), and (R_{{text{p}}}) are of utmost importance. The information requested is not included in the manufacturer’s datasheet. The data extraction process utilized a hybrid approach, combining an analytical method and a genetic algorithm (GA) as described in reference⁵³. Table 1 displays the datasheet parameters of the SM55 module, while Table 2 showcases the extracted parameters.

The meteorological variables, specifically temperature (T) and irradiance (G), exert influence on the extracted parameters^54,55,56:

DC–DC converter

To ensure impedance matching between the PV source and the load, the inclusion of a DC–DC converter is necessary in every MPPT system^54,57. This converter plays a crucial role in mitigating disturbances in our application by adjusting the voltage level. By doing so, it enables effective control of solar power generation even in the presence of partial shade. This capability allows the photovoltaic power output to align with the location of maximum global power. The converter utilized in this research paper is a SEPIC, as depicted in Fig. 1. The system is comprised of a coupling capacitor (C_{2}), an output capacitor (C_{1}), two inductors (L_{1}) and (L_{2}), a diode D, and a load resistance.

The DC voltage input is converted to the desired output voltage level through the energy exchange between the inductor (L_{1}), capacitor (C_{1}), and inductor (C_{2}). In general, the regulation of energy transfer is facilitated by a power transistor switch (S1), such as a MOSFET⁵⁸.

Based on reference⁵³, the state equations provided below can be utilized to depict the mathematical model of the SEPIC:

Regarding the variables of the GA and BSC, the following main statements are presented:

1. o

   (V_{pv}) represents the voltage at the output of the PV system

2. o

   (dot{V}_{pv}) represents the derivative with respect to time of (V_{pv})

3. o

   (I_{pv}) represents the current flowing at the output of the PV system

4. o

   (u) represents the control signal generated from the BSC

5. o

   (v_{ref}) represents the reference voltage generated by the GA.

The GA algorithms use a search heuristic inspired by Darwin’s theory of natural selection and species evolution. This algorithm simulates natural selection by simulating “survival of the fittest” across generations to solve a problem. Five stages make up a GA:

• Initial population: Each member has unique traits and characteristics. The decision-making process will depend on these variations, which vary in importance.

• Fitness function: a mathematical representation of an individual’s fitness level. Each person receives a numerical score from the fitness function based on demographics.

• Selection: Individuals will be chosen for reproduction based on their fitness rating. The genetically fittest can pass on their genes.

• The crossover process provides for two offspring by transferring assets between parents.

• The mutation: alters traits of an organism with a low probability of occurrence.

• Population convergence disables the algorithm. The GA offered multiple solutions.

Genetic algorithm parameters and their impact on optimization

In the following section, you will find some specifications on the Genetic Algorithm. These specifications aim to enhance your understanding of how specific parameters can affect the optimization process when utilizing the Genetic Algorithm.

1. 1.

   Population size:

   • Definition: The quantity of individuals (candidate solutions) in each generation of the genetic algorithm.

   • Impact: A larger population size typically leads to a wider range of solutions being explored during the optimization process. It has the potential to improve the algorithm’s global exploration capability, although it may necessitate additional computational resources. A smaller population size can lead to faster convergence, but it may also result in premature convergence to suboptimal solutions.

1. 2.

   Crossover Rate (Crossover Probability):

   • Definition: The likelihood of two individuals in the population engaging in crossover to generate new offspring.

   • Impact: A higher crossover rate encourages exploration by generating diverse solutions through recombination. On the other hand, if the value is too high, there is a risk of excessive exploitation, which could result in converging too quickly. A lower crossover rate promotes exploitation, which can lead to faster convergence towards promising solutions. However, it may also lead to a reduced diversity within the population.

1. 3.

   Mutation rate:

   • Definition: The likelihood of an individual’s genetic material undergoing mutation, resulting in unpredictable alterations.

   • Impact: Mutation plays a crucial role in maintaining genetic diversity by introducing random changes, which helps prevent premature convergence. An increased mutation rate promotes exploration while potentially impeding convergence if excessively high. An emphasis on a lower mutation rate can enhance exploitation, which has the potential to refine solutions. However, it may also result in a decrease in diversity.

1. 4.

   Selection mechanism:

   • Definition: The process of choosing individuals for reproduction is determined by their level of fitness.

   • Impact: Various selection mechanisms, like roulette wheel selection or tournament selection, impact the trade-off between exploration and exploitation. An effective selection mechanism ensures that individuals who are well-suited are more likely to pass on their genetic material to the next generation, thus driving the process of optimization.

1. 5.

   Termination criteria:

   • Definition: The criteria for the termination of the genetic algorithm include factors such as a predefined maximum number of generations or a desired fitness value to be achieved.

   • Impact: Having appropriate termination criteria helps avoid unnecessary computational costs. Establishing a practical limit on the number of generations guarantees that the algorithm will halt after a predetermined amount of work, while a desired level of fitness acts as a benchmark for satisfactory solutions.

1. 6.

   Elitism:

   • Definition: The preservation of the most capable individuals from one generation to the next.

   • Impact: Emphasizing the importance of excellence guarantees that the most effective solutions are passed down to future generations, safeguarding the potential of valuable genetic material. It has the potential to improve the speed at which solutions converge and the overall quality of the final results.

1. 7.

   Encoding scheme:

   • Definition: The different ways to represent solutions in the genetic algorithm include binary encoding, real-valued encoding, and permutation encoding.

   • Impact: The selection of encoding has a significant impact on the application of genetic operations such as crossover and mutation. The choice of encoding scheme should be carefully considered to ensure that it accurately reflects the nature of the optimization problem and allows for meaningful representations of solutions.

1. 8.

   Fitness function:

   • Definition: The objective function that measures the effectiveness of a solution.

   • Impact: The fitness function directs the genetic algorithm towards improved solutions. A precise fitness function should encompass the optimization objectives, offering a transparent metric for the algorithm to enhance.

Having a good grasp of and effectively adjusting these genetic algorithm parameters is essential in finding the right balance between exploration and exploitation. This will lead to reaching high-quality solutions without getting stuck in premature convergence. It is important to select parameters that are in line with the unique characteristics of the optimization problem to enhance repeatability and understanding. Experimentation and sensitivity analysis are frequently required to refine these parameters for optimal performance.

Proposed Genetic algorithm

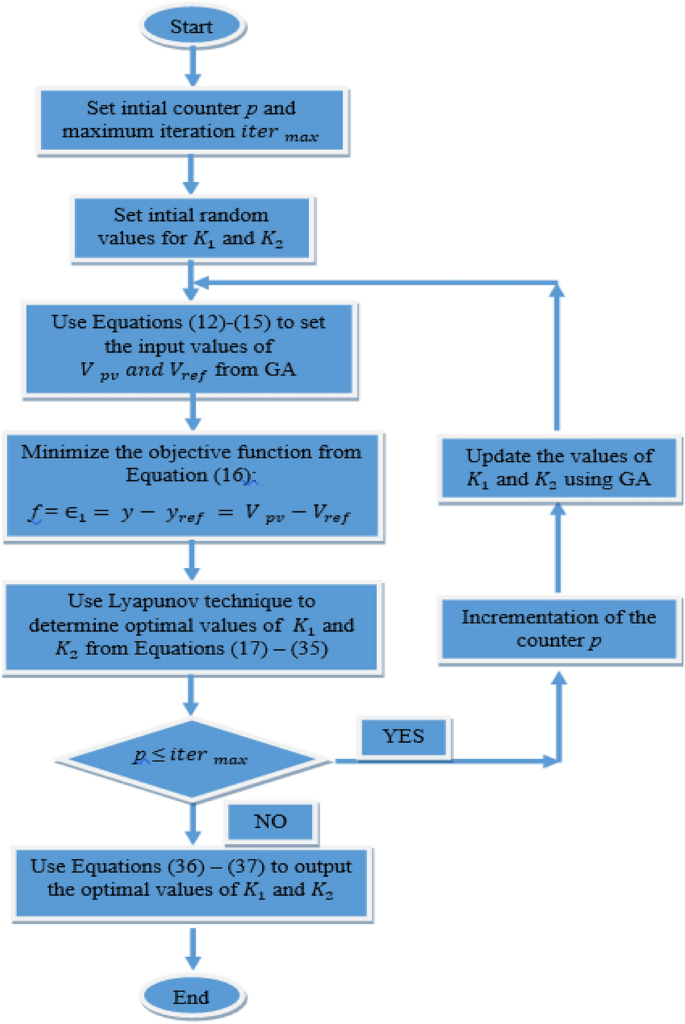
This study seeks to implement control mechanisms for a selected photovoltaic (PV) system. In this setup, a non-linear binary symmetric channel (BSC) receives a reference voltage generated through the genetic algorithm (GA). The controller employs a non-linear mathematical function to establish a control rule that is similarly non-linear. The rationale for employing a non-linear controller lies in the goal of precisely modeling the system to closely mimic its real-world behavior. In essence, the objective is to offer a comprehensive overview of the system’s operation under low-light conditions, aiming to achieve maximum power point tracking (MPPT) and fulfill load requirements. Flowchart of proposed Genetic Algorithm for BSC gains is shown in Fig. 2.

Flowchart of proposed Genetic Algorithm for BSC gains.

Full size image

Consequently, the control algorithm is assigned the task of adjusting the pulse width modulation (PWM) signal, which, in turn, governs the system’s operation through the utilization of a Single-Ended Primary Inductor Converter (SEPIC) connected to the load⁵⁹. The Genetic Algorithm (GA) is employed to compute the BSC gains, and, with the intention of achieving an optimal outcome.

The main objective is to ascertain the ideal voltage of the photovoltaic (PV) module, which is constrained within the range of 0 V and (V_{oc}). The primary goal of this objective is to ascertain the Global Maximum Power Point (GMPP)⁶⁰. The secondary objective is to identify the most suitable BSC parameters, denoted as (K_{1}) and (K_{2}).

Genetic algorithm MPPT

(K_{1}) And (K_{2}) the parameters of the BSC are determined by the GA, which is also responsible for generating the reference voltage. It is necessary to employ a vector consisting of six individuals in order to initiate the reference voltage. This vector extends from 0 V to the open circuit voltage, denoted as ({ }V_{oc}). The direct current to direct current converter receives one reference voltage at a time. The establishment of the ideal reference voltage makes it possible to reach and store the maximum amount of power on a global scale.

Elitism is used to select members of each generation after each member has been tested. The answer to this question can be found in the equation:

Unique mutations are extremely unlikely to occur. In order to make random changes to individuals during this stage, the algorithm employs the mathematical equation that is presented below:

where (v_{max}) and (v_{min}) are the search space’s voltage range upper and lower bounds. Both Eqs. (14) and (15) are utilized in order to put an end to the search for a reduction in mutation oscillations and to locate the reference voltage that is optimal across all generations. When the temperature or the amount of solar irradiation changes, the algorithm immediately restarts. When certain conditions are met, the GA does nothing:

GA-backstepping controller

Within this section, the nonlinear controller is implemented. The controller is responsible for generating the reference voltage, which is then utilized by the Genetic Algorithm in order to drive the PV system to its maximum power point. Additionally, the Lyapunov-based BSC controller is proposed in this paper.

First, define the primary tracking error, which is the difference between the real photovoltaic voltage and the GA’s reference voltage:

The time derivative of (in_{1}) is defined by:

Hence, by replacing the expression of (dot{V}_{pv}) from Eq. (11) as given in reference⁵³, Eq. (17) can be demonstrated as follows:

In order to ensure stability, the controller incorporates Lyapunov functions:

With (V_{1} left( { in_{1} } right) > 0).

The time derivative of (V_{1} left( { in_{1} } right)) gives:

In order to uphold Lyapunov stability, it is necessary for the time derivative of the Lyapunov function (V_{1} left( { in_{1} } right)) to be negative. In reality, that is feasible if this condition is met:

In order to adhere to the performance criteria, (K_{1}) is a positive parameter ((K_{1}) > 0) that can be chosen or computed. Given the virtual control (alpha_{1} = left( {I_{L1} } right)_{d}), it is assumed that this control allows for the stabilization of (in_{1}). Where (left( {I_{L1} } right)_{d}) represents the target value of the current flowing through the first inductor. Consequently, the virtual control (alpha_{1}) can be expressed using Eq. (21):

The next step involves the establishment of a precise definition for the second tracking error:

The Eq. (23) can be rearranged to obtain:

By substituting Eq. (22) into Eq. (24), we obtain:

Substituting the variable (alpha_{1}) with its corresponding numerical value yields:

Upon simplification of Eq. (26), we obtain:

Replacing (mathop { in_{1} }limits^{.}) in the Eq. (20)

The temporal rate of change of (in_{2}) can be expressed by utilizing Eq. (11) and Eq. (23):

where:

The incorporation of the second Lyapunov function (V_{2} left( { in_{1} , in_{2} } right)) is essential to guarantee the convergence of both errors to zero.

The partial derivative of (V_{2} left( { in_{1} , in_{2} } right)) with respect to time yields:

Taking into account the new expression of (mathop {V_{1} }limits^{.} left( { in_{1} } right)) from Eq. (28)

Consequently:

The following condition must be met in order to achieve Lyapunov stability, (mathop {V_{2} }limits^{.} left( { in_{1} , in_{2} } right)) must be negative, which implies the following condition has to be satisfied:

With (K_{2}) is a positive constant (K_{2} > 0) that presents a regulation parameter.

As a result, the real control is deduced based on Eq. (35), and Eq. (29):

Thus:

Which ensures converging (( in = in_{2} , in_{2})) asymptotically to 0. Thus, convergence of ({ }y) to (y_{ref}).

• The parameters (K_{1}) and (K_{2}):

The controller’s gains play a crucial role in shaping its response characteristics. Established tuning methodologies exist for PID-type controllers, providing guidance on determining the optimal gain values needed to achieve the desired response⁶¹. In contrast, there is a lack of a thoroughly established methodology for calibrating the gains of a backstepping controller.

In the GA, instantaneous values of (V _{pv}) and (I_{pv}) are introduced to generate the reference voltage for injection into the BSC. Thus, the initial values will lead to a random path that searches for optimal random values of parameters (K_{1}) and (K_{2}) to ensure system stability. In order to eliminate the search for a reduction in mutation oscillations and find the optimal reference voltage across all generations, Eqs. (14) and (15) are utilized. Whenever there is a fluctuation in temperature or solar irradiation, the algorithm promptly initiates a restart.

The proposed methodology employs a GA with the objective function of minimizing the voltage error ((in_{1})) to determine the optimal values of the BSC gains ((K_{1}) and (K_{2})).

The efficacy of the proposed hybrid GA-BSC is assessed through a series of experiments conducted using numerical simulations implemented in the MATLAB/Simulink platform. The PV array utilized in this study comprises three SM 55 W PV modules that are interconnected in a series configuration. The PV system is designed to operate at its maximum power point.

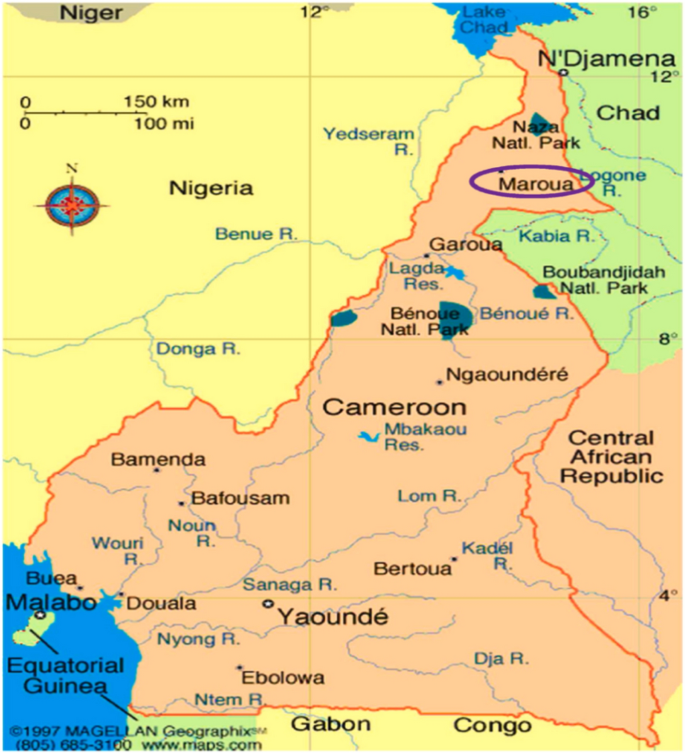
This study is conducted in the city of Maroua, situated at 10° 35′ North latitude and 14° 19′ East longitude, serves as the primary urban hub of the Far North region and Diamare division. The city boasts a population of about 1,007,000 inhabitants. Its climate is tropical, marked by aridity and high temperatures, akin to a semi-desert environment. The mean annual temperature registers at 28.3 °C, with an annual precipitation of 794 mm³. Figure 3⁴⁶ displays the city’s geographical coordinates. The recorded solar radiation in the region stands at around 5.80 kWh/m²/year, as noted in reference⁴⁷. The aforementioned factors have been duly considered for the case study, taking into account the simulation and aiming to replicate the most realistic conditions of the area. Therefore, there is a noticeable and significant rise in temperature in the specified area, characterized by arid conditions and high temperatures similar to those found in a semi-desert climate.

The map of Cameroon illustrates the geographical positioning of the city of Maroua⁴⁶.

Full size image

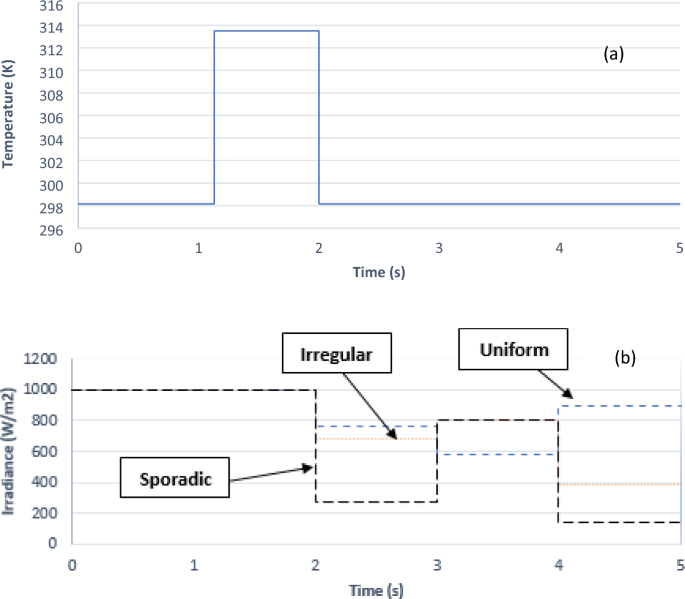
As a result of the inadequate performance of most MPPT algorithms in accurately following the GMPP during dynamic changes in operating conditions, we are conducting an investigation into the resilience of our systems in various climatic scenarios, both uniform and irregular, as depicted in Fig. 4. This investigation holds particular significance in the context of Maroua’s unique climatic conditions, characterized by high temperatures and sporadic weather patterns. The city’s semi-desert environment and solar radiation levels play a critical role in shaping the behavior of photovoltaic systems. Therefore, our research aims to validate the adaptability of the proposed algorithm to the challenging and diverse climate of Maroua. By subjecting our algorithm to a range of climatic scenarios, we seek to ascertain its capacity to consistently track the GMPP and optimize energy extraction, ensuring a viable and effective solution for the local photovoltaic infrastructure. During the time period from 0 to 2 s, the irradiation was maintained at a constant level of 1000 watts per square meter for all three PV modules. In the subsequent time period from 2 to 5 s, the irradiance was intentionally varied for the three PV modules to simulate partial shading conditions.

Meteorological conditions: (a) temperature; (b) solar irradiance.

Full size image

For the temperature, it was 298.15 K between 0 and 1.13 s, 2 to 5 s, and it increased to 313.5 K between 1.13 and 2 s.

The proposed approach utilizes a GA to generate the reference voltage and determine the optimal gains (K_{1}) and (K_{2}) for the BSC. The reference voltage is utilized by the nonlinear BSC to optimize the operation of the PV System at its maximum power point. The system comprises a SEPIC, and its specifications are presented in Table 3.

The proposed hybrid method is first evaluated under standard test conditions (STC), within the time interval [0 s, 1.13 s]. These conditions correspond to an irradiance of 1000 W/m² and a temperature of 25 °C.

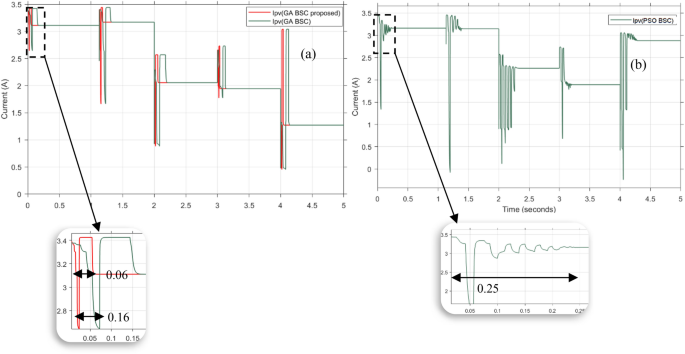
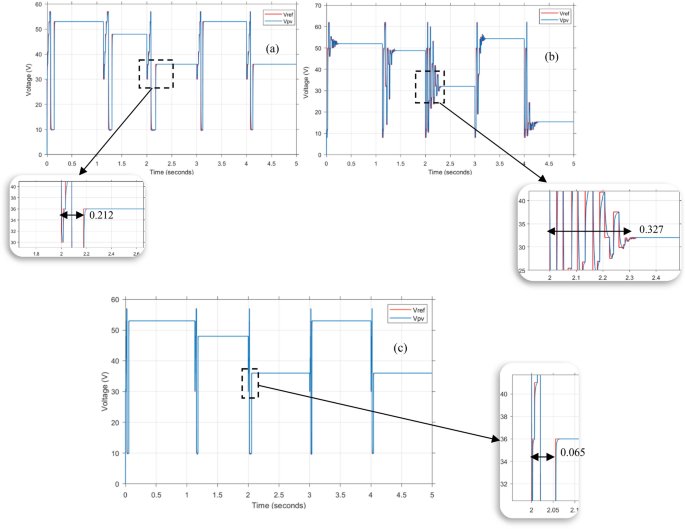
Figures 5 and 6 depict the photovoltaic current and voltage of the PSO algorithm with BSC modulation. The method³¹ demonstrates BSC gains in Table 4, where (K_{1}) = 435 and (K_{2}) = 500. Both the GA with BSC and the proposed method utilize the same gains as the PSO method. In the proposed method, the values shown in Table 4 are used as the initial proposed values for the gains (K_{1}) and (K_{2}), following the flowchart explained in Fig. 2. In the proposed method, the optimal values of the gains for the BSC controller are determined using GA.

Photovoltaic current for GA-BSC, GA-BSC proposed (a), and PSO-BSC (b).

Full size image

Photovoltaic voltage for GA-BSC (a), PSO-BSC (b) and GA-BSC proposed (c).

Full size image

The figures demonstrate the effectiveness of the GA-BSC technique, which involves using a GA to calculate the optimal values for the parameters (K_{1}) and (K_{2}) in the BSC. By employing this technique, the photovoltaic voltage can closely and quickly track the reference voltage, leading to minimal oscillations. The proposed GA-BSC method stands out from other methods due to its impressive ability to achieve stabilization in a remarkably short time of just 0.065 s. However, the proposed method outperforms the GA-BSC method with nonoptimal gains in terms of time efficiency. It only takes 0.212 s, which is less than one-third of the time required by the GA-BSC method. In a rather unfortunate turn of events, the PSO-BSC method exhibits a considerably longer stabilization time of 0.327 s, a duration that is eight times lengthier than the proposed method.

The photovoltaic current exhibits a similar pattern of behavior. The proposed technique achieved stabilization in just 0.06 s, while the method took 0.16 s, more than twice as long as the proposed approach. Furthermore, the PSO-BSC method took 0.25 s to complete, which is four times longer than the proposed method.

The voltage error data for the three different methods can be found in Table 5. Based on the comparison of error performance between the GA-BSC method and the PSO-BSC method, it can be concluded that the GA algorithm is more effective than the PSO algorithm in accurately tracking the MPP.

When compared to the same method with subpar gains, the proposed method showcases a significantly lower error, highlighting its superiority. The improved performance of the proposed method is evident when gains are computed using GA. The importance of using optimal gains for controllers in all methods is highlighted by this.

• Evaluation of the proposed hybrid system at STC.

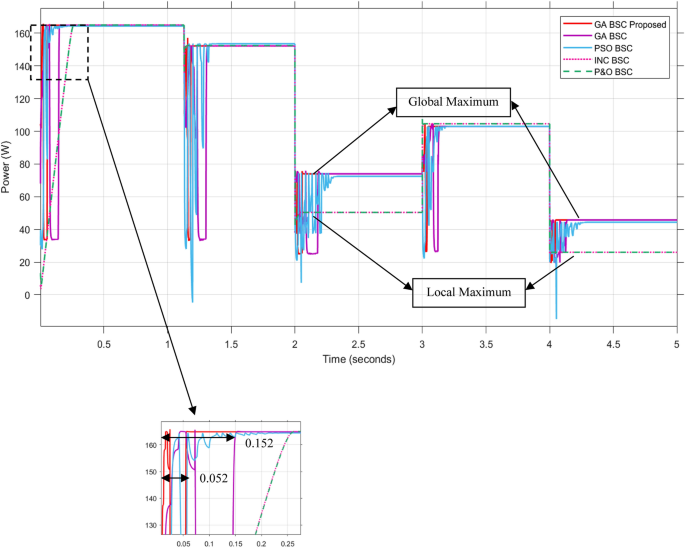
Given the specifications outlined in Table 1, it is expected that the PV module under examination will have a maximum power output of 165 W and a maximum voltage of 52.2 V in the given conditions. The simulation results are depicted in the subsequent figures:

Figure 7 depicts the monitoring of the MPP power as the systems undergo the aforementioned scenarios. The power figure illustrates the robust MPP tracking capability of the recommended hybrid system. The proposed hybrid approach utilizes the calculated BSC Parameters (K_{1}) and (K_{2}) to achieve stability at the MPP within 0.052 s. In comparison, the GA-BSC method with non-optimal (K_{1}) and (K_{2}) (as shown in Table 4) takes 0.152 s to reach the MPP, which is three times longer than the proposed method. Additionally, the P&O-BSC and INC-BSC methods require 0.252 s, which is five times longer than the proposed method.

Comparison of MPPT and GMPPT techniques under various meteorological conditions. Figure 8 Comparison of MPPT and GMPPT techniques under STC.

Full size image

• Additional discussions.

When setting up the gains in a Backstepping controller, it is crucial to take into account multiple factors and make thoughtful decisions to balance different considerations. The main parameters that need adjustment are the proportional gain ((K_{1})), the integral gain ((K_{2})), and possibly other system-specific parameters. Here are the main considerations when configuring Backstepping controller gains:

1. 1.

   Convergence Speed vs. Stability:

   • Trade-off: Increased values of ({K}_{1}) and ({K}_{2}) typically result in quicker convergence, as the control input becomes more responsive to errors.

   • Consideration: Nevertheless, an excessively high gain could potentially affect stability. Quick adjustments to the control input can result in overshooting and oscillations, which can potentially lead to instability.

1. 2.

   Steady-State Error vs. Convergence Speed:

   • Trade-off: By increasing ({K}_{2}), the steady-state error can be reduced as it amplifies the correction for accumulated errors over time..

   • Consideration: Finding the right balance between speed and accuracy is essential. Significantly high ({K}_{2}) values can decrease steady-state error, but they may also hinder convergence by placing too much emphasis on past errors.

1. 3.

   Resilience under Disturbances vs. Convergence Speed:

   • Trade-off: Increasing ({K}_{1}) and ({K}_{2}) can improve the system’s ability to handle disruptions and reduce their negative effects.

   • Consideration: However, responding strongly to disruptions can sometimes result in unnecessary control actions, which can cause oscillations or instability. Emphasizing resilience might result in a less seamless response.

1. 4.

   Noise Sensitivity vs. Steady-State Error:

   • Trade-off: An elevated ({K}_{2}) value can effectively mitigate steady-state error resulting from external disturbances or noise.

   • Consideration: However, this could potentially increase the controller’s susceptibility to system noise. Finding the right equilibrium is crucial to maintain resilience against disruptions while minimizing the impact of interference.

2. 5.

   Smoothness of Control Input vs. Rapid Transients:

   • Trade-off: Reducing the gains leads to smoother control inputs, which in turn decreases the chances of sudden changes.

   • Consideration: However, reducing gains may result in slower convergence speed and less responsiveness. The task at hand is to discover improvements that achieve a harmonious blend of fluidity and swift adjustment.

1. 6.

   Robustness under Parameter Variations vs. Convergence Speed:

   • Trade-off: Increased gains can improve the controller’s capacity to adjust to changes in system parameters.

   • Consideration: Significant variations in parameters can cause instability if there are excessive gains. Finding the right balance between robustness and convergence speed is of utmost importance when tuning gains.

1. 7.

   Control Effort vs. Stability:

   • Trade-off: Greater gains typically necessitate increased control effort in order to attain the desired level of performance.

   • Consideration: When it comes to maintaining stability and responsiveness, it is crucial to keep the control input within acceptable limits to prevent saturation or other practical limitations.

1. 8.

   System-Specific Characteristics vs. Generic Tuning:

   • Trade-off: Standard gain tuning may not take into consideration the unique characteristics or limitations of the controlled system.

   • Consideration: Customizing gains to match the unique dynamics of the system can improve performance, although it necessitates in-depth understanding and may not be applicable to different systems.

To summarize, the process of setting up Backstepping controller gains requires careful consideration of multiple factors, including convergence speed, steady-state error, resilience, noise sensitivity, and other relevant aspects. The task at hand is to discover gain values that achieve a harmonious equilibrium and enhance the controller’s performance across various operating conditions. It is often necessary to go through a process of iterative tuning and testing in order to achieve the desired trade-offs for a specific system.

• Assessment of the Proposed Hybrid System under diverse meteorological conditions.

The hybrid method system that was proposed is currently functioning in conditions that are extremely unfavorable by any means. The purpose of this test is to determine whether or not the proposed MPPT system is feasible, as well as to assess the system’s enhanced capacity to withstand operational conditions that are challenging.

Figure 8 presents a comparative analysis of MPPT and GMPPT techniques. Specifically, the techniques being compared are INC-BSC, PSO-BSC, P&O-BSC, and GA-BSC. The comparison is conducted in various weather conditions throughout the process. The figure presented provides a visual representation of the benefits offered by the proposed method in different weather conditions. Furthermore, it highlights the drawbacks of alternative MPPT methods when applied in non-uniform meteorological environments. The proposed approach, similar to the Standard Test Conditions (STC), showcases enhanced efficiency in swiftly tracking and stabilizing at the Maximum Power Point (MPP) when compared to alternative methods. Furthermore, it can accurately monitor the GMPP in various conditions, including uniform and particle shading. However, the MPPT approaches, particularly the P&O-BSC and INC-BSC, exhibit noticeable oscillations when faced with variations in temperature and irradiance. These methods are unable to accurately track the General Maximum Power Point (GMPP) in the presence of partial shading. Instead, they converge to the Local Maximum Power Point (LMPP). The proposed method significantly reduces power consumption by 33 percent compared to other methods, resulting in a notable decrease in power usage.

On the other hand, the GA approach demonstrates superior efficiency and has the potential to serve as a replacement for the PSO algorithm due to the fact that it has a faster computational speed in comparison to the PSO algorithm. The GA-BSC method that was proposed allows for the determination of the parameters (K_{1}) and (K_{2}) of the BSC through the use of a GA. The GA-BSC method is improved in terms of both speed and accuracy when compared to the PSO-BSC method and the use of nonoptimal gains when this approach is utilized.

• Stability analysis:

According to the flowchart depicted in Fig. 2 and considering the objective function presented in Eq. (38), the following points can be considered in order to justify the stability analysis performed using the BSC:

• Ensuring Stability: The use of Lyapunov functions in stability analysis provides a solid basis for guaranteeing the stability of the Backstepping controller. Through the demonstration of the negative definiteness of the time derivative of the Lyapunov function (Eq. 37), we can confidently assert that the closed-loop system will converge to the desired equilibrium point when influenced by the Backstepping control law.

• Robustness Analysis: After conducting a thorough evaluation, it is evident that the Backstepping controller demonstrates impressive resilience in the face of uncertainties and disturbances. The analysis took into account different system parameters and disturbances, showing that the controller is able to maintain stability and satisfactory performance in various operating conditions (Figs. 5a and 6c). This level of robustness is essential for practical applications, as real-world systems frequently face uncertainties.

• Disturbances rejection: The Backstepping controller demonstrates remarkable effectiveness in rejecting external disturbances. The controller’s main objective is to maintain a stable and reliable performance by reducing the effects of disturbances in the closed-loop system.

• Sensitivity analysis:

Based on the flowchart shown in Fig. 2 and taking into account the objective function described in Eq. (38), we can consider the following points to discuss the sensitivity analysis of our system using the proposed BSC. This will help evaluate the sensitivity of the Backstepping controller to changes in the gains ((K_{1}) and (K_{2})) and gain a better understanding of the method’s resilience under different parameter settings:

• Initial Parameter Setting: Set the initial values for (K_{1}) and (K_{2}) based on the design of the Backstepping controller. This process is performed in a randomized manner to maintain the dynamic nature of the system.

• Define Sensitivity Range: It is necessary to define a range for the variations in the gains ((K_{1}) and (K_{2})) that will be examined. Thorough analysis has been conducted to address both favorable and unfavorable fluctuations, ensuring the system’s stability.

• Performance Metrics: In order to accurately assess the effectiveness of our proposed method, it is crucial to establish appropriate performance metrics for measurement. In this work, we have taken into account the voltage error, as indicated in Table 5. The proposed method demonstrates a satisfactory level of voltage error when compared to other methods that have been studied.

• Vary (K_{1}) and (K_{2}): During simulations, it is important to systematically vary the values of (K_{1}) and (K_{2}). We have conducted simulations of the system and observed the response for each combination of (K_{1}) and (K_{2}), as indicated by the flowchart. While ensuring the system maintains stability, the loop continues until the maximum iteration exit condition is met.

Studying the sensitivity to changes in the Backstepping controller gains offers valuable insights into the method’s resilience and helps in choosing the best gain values. Having a clear grasp of how the system reacts to changes in (K_{1}) and (K_{2}) is essential to guaranteeing reliable performance under various operating conditions.

• Perspectives of the work:

In response to the widespread adoption of various Maximum Power Point Tracking (MPPT) methods, researchers and practitioners have conducted surveys and comparisons of photovoltaic systems. Both fuzzy logic and artificial neural networks exhibit the capability to track Maximum Power Points (MPPs). However, achieving the appropriate inference mechanism, rule base, and offline statistics training data process requires a well-designed system architecture. Despite the inclusion of operator skills, inference rules, and membership functions, errors may still occur within the controller.

In the present day, heuristics are utilized for optimizing MPPT in scenarios involving partial shade, necessitating the application of intricate mathematical algorithms. The intricacy of these algorithms can pose challenges in implementation procedures. Therefore, to validate the proposed simulation in our study, it is crucial to consider the potential for conducting future experiments.

• Some barriers for the implementation of the work:

Identifying challenges in implementing the proposed backstepping controller in a real-world scenario can involve considering the following factors:

• Sensor Noise:

  1. o

     Challenge: Noise is introduced into measurements by real-world sensors, which can have an impact on the accuracy of feedback signals.

  2. o

     Mitigation: Apply signal filtering techniques or employ sensor fusion methods to minimize the influence of noise. Take into account the utilization of Kalman filters or alternative algorithms for reducing noise.

• Hardware Restrictions:

  1. o

     Challenge: Practical hardware often faces limitations when it comes to processing power, memory, or communication speed.

  2. o

     Mitigation: Improve the algorithm to enhance computational efficiency, taking into account the limitations of the hardware. Utilize hardware-in-the-loop simulations to verify the controller’s performance within practical hardware constraints.

• Actuator Dynamics:

  1. o

     Challenge: Physical actuators can exhibit dynamics that deviate from the ideal model assumed in the Backstepping controller design.

  2. o

     Mitigation: Include the actuator dynamics model when designing the controller. Apply advanced control techniques to effectively manage uncertainties in the actuator’s behavior.

  3. o

     Nonlinearities in the System:

  4. o

     Challenge: Real-world systems frequently display nonlinearities that can deviate from the assumed model.

  5. o

     Mitigation: Utilize adaptive control techniques to dynamically adjust the controller parameters in response to observed nonlinearities. Perform a comprehensive system identification to gain a deep understanding and accurately model the nonlinear aspects.

  6. p

     Parameter Uncertainties:

  7. o

     Challenge: Fluctuations in system parameters have the potential to impact the efficiency of the Backstepping controller.

  8. o

     Mitigation: Implement strong control techniques to effectively manage uncertainties. Utilize parameter estimation techniques to consistently update the controller parameters using real-time measurements.

  9. q

     Environmental Variability:

  10. o

      Challenge: Modifications in environmental conditions, such as temperature or humidity, have the potential to affect system dynamics.

  11. o

      Mitigation: Develop and apply control strategies that can dynamically modify the controller parameters in response to real-time environmental feedback. Take into account environmental monitoring systems to supply the controller with pertinent information.

Addressing these implementation obstacles ensures that the Backstepping controller remains effective and reliable in real-world scenarios, considering the complexities and uncertainties inherent in practical applications. Thorough testing, validation, and continuous monitoring are essential to ensure the controller’s robust performance under diverse and challenging conditions.

• Some benefits for the implementation of the work:

Utilizing the proposed GA-BSC Approach to address non-uniform irradiance will have many benefits. Nevertheless, it is crucial to address certain obstacles concerning the precision of the system:

• ** Challenge:

The performance of solar tracking algorithms can be significantly affected by non-uniform irradiance, which is caused by the variation in solar radiation across the tracking system. Poor tracking accuracy can result in less effective energy harvesting and decreased efficiency of the entire system.

• ** Consequences for Tracking Accuracy:

Uneven distribution of irradiance poses difficulties like the presence of shadows, partial cloud cover, and fluctuations in sunlight strength. These factors may cause inaccuracies in estimating the solar position, which can result in tracking errors. The accuracy of the tracking system can have a significant impact on the energy output of the solar panels and potentially undermine the expected efficiency improvements from solar tracking.

• ** Strategies Implemented in GA-BSC:

The proposed approach, which combines Genetic Algorithms (GA) with Backstepping Control (BSC), provides inherent advantages for dealing with non-uniform irradiance:

• Genetic Algorithm for Parameter Tuning:

The adaptability of GA enables it to dynamically optimize the parameters of the Backstepping controller. The adaptability of the system allows for the adjustment of the tracking algorithm to accommodate variations in irradiance conditions.

• Backstepping Control for Nonlinear Systems:

BSC is specifically designed to address the complexities in the system dynamics. The system has the ability to seamlessly adjust to variations in irradiance levels, allowing it to effectively handle situations where irradiance is not uniform.

• Parameterized Control Policies:

The genetic algorithm is capable of evolving parameterized control policies within the Backstepping framework. The controller is designed to easily adjust to changes in irradiance patterns, which helps to minimize any tracking errors that may occur.

• Population Diversity in Genetic Algorithms:

The wide range of individuals in the GA population enables the opportunity to investigate various control strategies. As the conditions of irradiance fluctuate, the GA has the ability to adjust by giving preference to individuals in the population who have control policies that excel in situations with varying levels of irradiance.

• ** Potential Strategies for Future Development:

In order to improve the effectiveness of the proposed GA-BSC approach in dealing with varying levels of irradiance, it would be beneficial to consider the following strategies for future development:

• Dynamic Parameter Adaptation:

Develop a method to adjust the parameters of the Backstepping controller in real-time using measurements of irradiance. This guarantees ongoing optimization in light of evolving environmental conditions.

• Incorporation of Environmental Sensors:

Add environmental sensors, such as pyranometers, to the system for immediate feedback on irradiance levels. This data can be utilized to enhance the GA-BSC approach and enable more precise tracking.

• Machine Learning Integration:

Discover the incorporation of machine learning algorithms to forecast and adjust to varying irradiance patterns. By implementing this solution, the controller will be able to more effectively adapt to fluctuations in solar conditions.

• Hybrid approaches:

Discover the incorporation of machine learning algorithms to forecast and adjust to varying irradiance patterns. By implementing this solution, the controller will be able to more effectively adapt to fluctuations in solar conditions.

• Experimental validation:

Perform thorough experimental validation across a range of irradiance conditions to optimize the parameters of the GA-BSC. Practical testing will offer valuable insights into the performance of the controller and help inform future enhancements.

The proposed GA-BSC approach shows great potential in dealing with the challenges of non-uniform irradiance by being adaptable and capable of optimization. Through the exploration of various techniques and approaches, future advancements have the potential to greatly improve the reliability and efficiency of the GA-BSC method in practical solar tracking scenarios. Continuous validation and refinement based on real-world field performance will be crucial to guaranteeing its success in a variety of environmental conditions.

In response to the widespread adoption of various Maximum Power Point Tracking (MPPT) methods, researchers and practitioners have conducted surveys and comparisons of photovoltaic systems. Both fuzzy logic and artificial neural networks exhibit the capability to track Maximum Power Points (MPPs). However, achieving the appropriate inference mechanism, rule base, and offline statistics training data process requires a well-designed system architecture. Despite the inclusion of operator skills, inference rules, and membership functions, errors may still occur within the controller.

This study aimed to develop a Maximum Power Point Tracking algorithm that could accurately identify and track the global maximum power point in various operational scenarios. The method relies on a Genetic Algorithm-Backstepping controller fusion tailored to Maroua’s solar dynamics.

The Genetic Algorithm served two purposes in this method. First, it consistently generated a reference voltage that fit Maroua’s environment. Second, it optimized the Backstepping controller’s integral coefficients K₁ and K₂. Real-time SEPIC converter management by the Backstepping controller maintained a consistent reference voltage.

The proposed technique was extensively evaluated to validate it. These included GA-BSC, PSO-BSC, P&O-BSC, and INC-BSC comparisons. MATLAB/Simulink simulations showed that the P&O-BSC and INC-BSC methods tracked the maximum power point under constant climate conditions but failed under partial shading. They followed the LMPP, which could cause power outages.

In contrast, our method accurately detected and mitigated partial shading effects, aiming for the global maximum power point to minimize energy loss. The GA-BSC configuration with genetically fine-tuned K1 and K2 parameters converged at the GMPP three times faster than its non-optimized version and five times faster than the P&O-BSC and INC-BSC configurations. This stressed the importance of calibrated controller gains.

A direct comparison between GA-BSC and PSO-BSC showed the former’s advantages in speed, stability, and reliability, which are essential in Maroua’s dynamic solar setting. Simulating a 33% reduction in power loss and a capitalization less than three times comparable stability methods shows significant advantages. Our model’s resilience is exceptional.

Modern partial shade MPPT optimization uses heuristics and complex mathematical algorithms. Complex algorithms can make implementation difficult. Our simulation needs to be validated by future experiments. Indeed, as perspectives, researchers and practitioners have compared photovoltaic systems since MPPT became popular. Max Power Points can be tracked by AI and fuzzy logic. The right inference mechanism, rule base, and offline statistics training data process require a good system architecture. Controller errors can occur despite operator skills, inference rules, and membership functions.